weblog
list of entries
how to program in unary
20200614
It is possible to write any computer program in a unary language. This is a language whose character set is of size 1.
Instead of a binary system (e.g., digits 0 and 1), a unary system has only a single ut, or unary digit (binary: bit; unary: ut). I have decided here to use the 0 character. Instead of a traditional, positional numeral system of radix n, where n is a positive integer, it is necessary to define a new system, where zeroes can be placed together in order to present a number. This is because n to the 0th power consistently equals 1.
The new system is based only on length, where the length n corresponds to the number it represents. For example, the unary '000' equals '3' in base-10; an empty utstring would thus equal zero.
In order to translate a computer program (or any string of ASCII characters) into a unary representation, the string is first converted into its nondelimited binary representation and optionally converted into decimal. This number represents the number of uts in its unary expression. Take, for example, the following 22-byte C one-liner.
void main(){return 0;}
This is converted to nondelimited binary.
01110110011011110110100101100100001000000110110101100001011010010110111000101000001010010111101101110010011001010111010001110101011100100110111000100000001100000011101101111101
The unary representation is thus ~4.43·1052 uts in length, representing an untenable file size.
quandaries with copyleft
my take on the state of the free software movement
20190712
There is a great, unknown enemy of the free software movements of this technological age. It is not Microsoft; it is not even the U.S. government; it is the attempted free license, the ironically restrictive license which is championed by some to grant freedom but which in fact hinders it.
There are several examples of this which I have found, the most horrible being the copyleft and its derivatives. Instead of a complete rejection of the ideas and purposes of copyright, copyleft creates its own restrictions that deprive the user of absolute freedom.
Copyleft unironically and earnestly claims, in a facade of freedom, that the material is not restricted, that anyone may use it in any way, distributing it, modifying it, blah blah, but that this license not be removed from the software or any modified or extended versions.
The intention of copyleft is clear: that these monstrously evil companies that we have come to know and hate, CEOs maniacally laughing at every uninformed purchase of Excel or Photoshop, not have the right to use this free software in their corporate products, which would supposedly go against the popularization and adoption of free alternatives in their benefit. Not only do they not give a damn about this insignificant piece of text, as their software can never be screened for compliance with RMS's sort-of-libertarian dreamwork (however, the impotence of this nonsense is not at all the focus or even a supportive point of my argument), but in actuality the effort to promote the production and adoption of free software is pretty simple: to produce it and to allow its use in every way absolutely, without restriction. Yes, I know it is unimaginable to not restrict something.
So-called "permissive" licenses, like ISC, MIT/X11, zlib, et cetera get the bullet too, although infinitesimally so, as they usually do not place copyleft restrictions on software derivatives.
Licenses like this invoke the power of the state just as copyright does, preventing absolutely free use of the material for any purpose. This does not reject the state and corporate power-by-extention-of-the-state, but it utilizes it just as importantly, (attemptedly) ensuring that there are legal grounds to punish perpetrators for misuse of the material.
Fortunately, there are people who get it. Rob Landley, the author of the Zero-Clause BSD license (formerly Free Public License 1.0.0) created the perfect license. It does exactly what is necessary in a governmental system where someone can find grounds to sue a producer for just about any reason: it states erasure of liability for the producer. Unlicense does this and a little more. Arto Bendiken excellently articulates the underlying philosophy of the Unlicense: it does what the 0BSD does, with the added declaration of dedication of the material to the public domain. This is something which should be implied but which "some backward jurisdiction," as he puts it, might not see.
Without making this post an all-encompassing rambling about the various esoteric licenses, here are some comments on a few that I have seen. The WTFPL comes close to being free, but I would have excluded the name-change clause just for the sake of absolutism. Additionally, I will probably never be buena onda, but this one is kind of cute. Finally, the maximal CC0 sucks (as any license that it takes two years to write does). I am fairly certain that there are plenty more fun licenses that I have not mentioned which would evoke plenty of indignant huffs from Stallman and chuckles from people with a sense of humor, but I have not looked into them.
But how can authors possibly gain recognition without their names splattered all over the source code? How can one ever make the claim that a new feature of Windows started as free software? In order to prevent someone from distributing their software under your software's name or distributing your software under a different name, in essence, to prevent undue credit, let's take a different approach. It is my belief that, instead of using a restrictive license, it is the responsibility of the original author to publish indisputable proof of their authorship in order to take credit and dispel false blame for unforeseen mishaps (e.g., erroneous use of the software and a subsequent lawsuit).
So far, I have not come across a simple solution to this problem that is accessible and (inb4 Wayback Machine) not centralized. An authorship system could be designed using blockchain or a similar technology such that an individual can publish material which is undeniably linked to a particular time and identity (i.e., through a key pair) within a decentralized system. Maksym Trilenko and several researchers have already proposed this idea. However, as far as I have looked, there does not seem to be a popular or even usable implementation of this yet. This should be soon-to-come.
The conversation about this concept is altogether very quiet. The importance of authorship from an individualist standpoint is powerful, and not enough recognition is given to recognition. People can make money from their proprietary software, but just give me a place in history.
Free software should actually be free. Make the right choice when publishing open-source material, and place it in the public domain, with or without a license. Unencumber your software.
quantification of bitstring randomness
an uncomplicated method by which to quantify bitstring randomness based on comprised repetition
20180112
The maximum number of transitions from 0 to 1 or from 1 to 0 within a bitstring of a given length, n, equals n minus 1. There is also an ideal number of transitions, which is the maximum divided by 2. his would be expressed as follows:
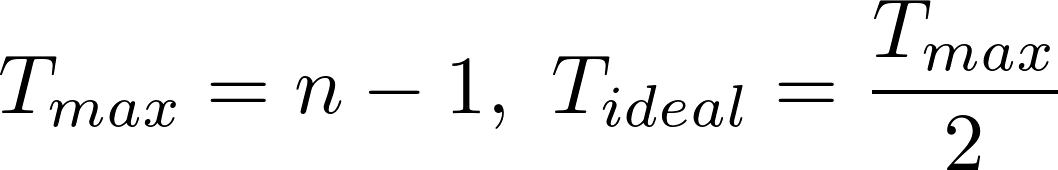
A bitstring with exactly Tmax transitions would be an alternating 0-1-0-[..] or 1-0-1-[..] bitstring, with an absolutely predictable order. A bitstring with zero transitions, i.e., 0-0-0-[..] or 1-1-1-[..], will also have absolute predictability.
Bitstrings with exactly Tideal transitions will be the most unpredictable, because each pair of bits has exactly the same probability of containing a transition or not.
In order to create an expression that will return the randomness of a bitstring, by these terms, the ratio of the actual number of transitions to the ideal will be taken into account.
This ratio will have a certain distance from 1, showing how far from ideal it is. This is squared in order to accentuate predictability at larger distances from 1 and for symmetry about 1. This value is subtracted from 2, and the base-2 logarithmic value of this is taken in order to generate an output value that will be closer to 0 when the input approaches 1 and an output of 1 when the input approaches 2, where the higher value shows a higher randomness. The full expression is as follows:
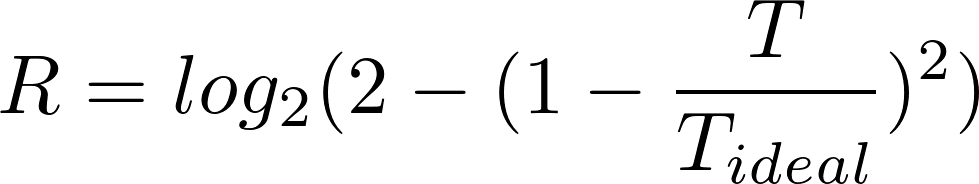
In order to grasp what shape this expression produces for proportion of transitions in a sufficiently large bitstring, the following function is constructed:
![f(x) = log_2(2 - (1 - x / T_ideal) ^ 2), {x in Z : x in [0, T_max]}](img/bitstring-function.png)
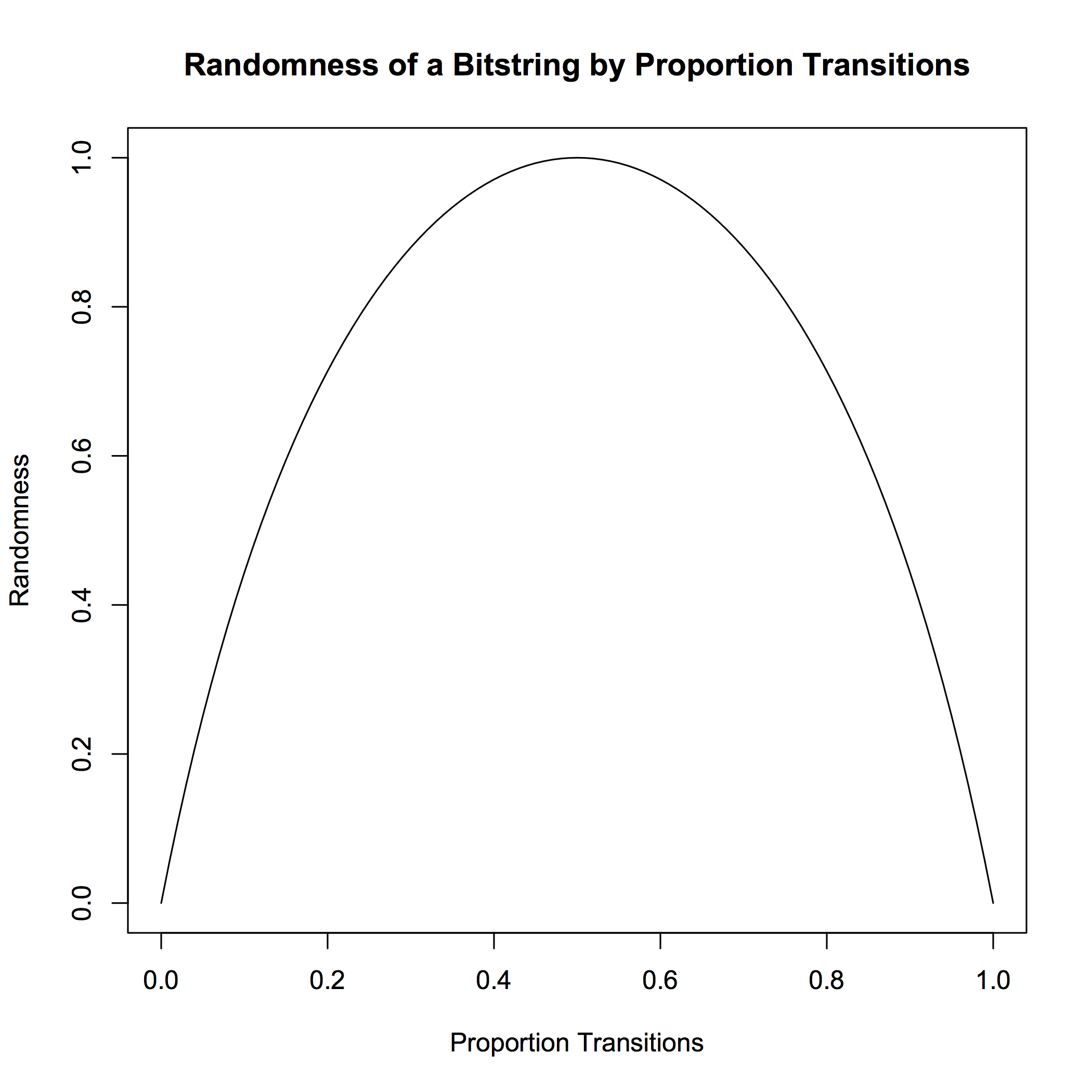
When this function is plotted over the range of possible transitions for a given bitstring, the following curve arises, with values of 0 given for bitstrings with the least ideal proportions of transitions and a value of 1 given for the ideal proportion of transitions, 0.5:
However, in merely using this expression, it can be found that clearly predictable bitstrings can be easily constructed which would be shown to have very low predictability, based on the score given, for example:
1100110011001100
This bitstring would be given the score of 0.99, a very high score for a bitstring with perfect predictability. The fact that almost a perfect number of transitions exist in this bitstring causes it to be judged as highly unpredictable, although these transitions are placed very predictably from each other.
In order to create a program that would judge this, justly, as the predictable bitstring that it is, another approach must be taken. I have proposed a way to evaluate bitstrings such that all ways of organizing it consistently will be examined, and the lowest score achieved will be assigned to this bitstring as a more correct score.
The bitstrings are broken up into segments of variable length, and each bit is taken and placed into a new bitstring in the order that they appear in the given segments. All segment lengths ranging from 1 to the length of the bitstring are tested. However, it is unnecessary to test beyond segment lengths of the length of the bitstring divided by 2, because these rearrangements are the bitstring itself. For example, the bitstring above would be tested in segments of all lengths ranging from 1 to 8.
This bitstring will be separated into segments of a given length (e.g., 2). The first bit of each segment will be taken, and then the second bit of each segment will be taken. The resulting concatenated bitstring is evaluated. Following the 2-length example, the process is outlined in the following image:
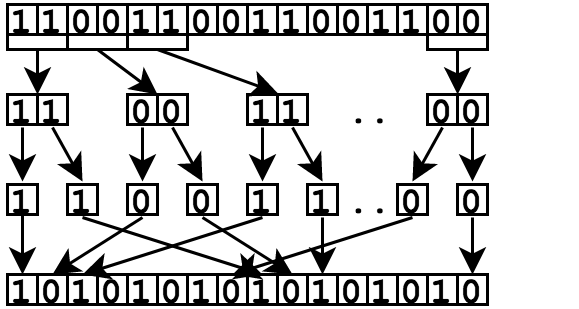
In this example, the bitstring is evaluated to the score of 0.00, because there are a maximum number of transitions possible in this consistent arrangement.
Similarly, using this same type of evaluation on a longer bitstring, the binary representation of the ASCII string This is an encoded ASCII string.:
0101010001101000011010010111001100100000011010010111001100100000011000010110111000100000011001010110111001100011011011110110010001100101011001000010000001000001010100110100001101001001010010010010000001110011011101000111001001101001011011100110011100101110
If evaluated without rearrangement, this bitstring would be given a score of 0.99. However, the consistency in ASCII character binary representations allows for a less random bitstring to be created when bits are taken in order from segments of length 8:
0000000000000000000000000000000011110110110111111101111101111110011111111111111111100000111111111001001000000000000010000111000001100100010010100000001100001101100000000101101111000000001001110001001001001110000011000101011100110110100101101001111101001010
Because of the lower randomness of this bitstring, a lower score of 0.92 is given. The lowest score generated from the computation of randomness scores for rearrangements of any possible length—also known as the rearrangement parameter—is assigned to the bitstring.
If we define a bitstring as an n-tuple, for example:
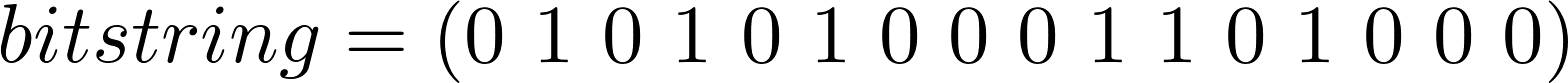
A set of all indices within this n-tuple—also the set rearrangement parameters—is defined:
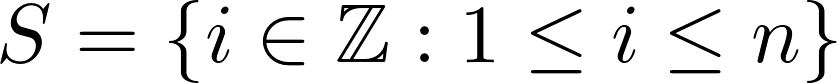
Then the bistring can be rearranged using the process described above using a mathematical formula. The actual rearrangement of the bistring, given in the form of a piecewise function is as follows:
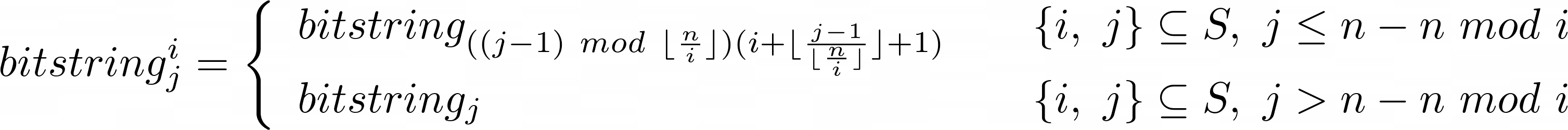
I found a hack that allows the index formula in the first piece to be somewhat simplified (note the change in conditionals):
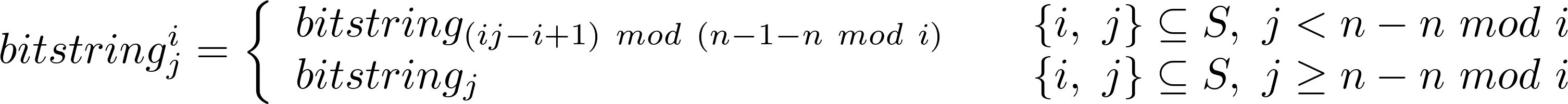
In order to calculate the number of transitions in each rearrangement, the following function is used:

Here, I have used a sumation of the negated equality comparison of each pair within the bistring to give the number of transitions within the bitstring. A randomness score is then taken for each rearrangement, and the minimum value generated from rearrangement for any i in S, is calculated:
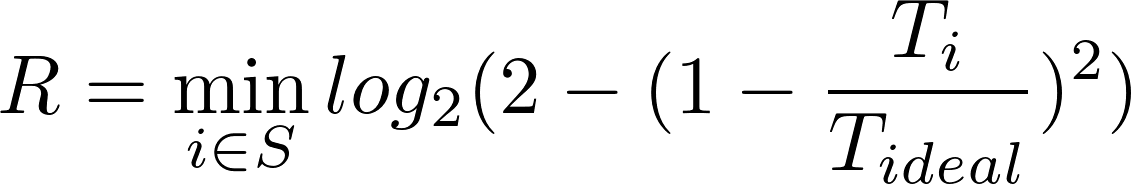
The future applications of this development are currently unclear, but I contend that the scores these bitstrings are given by this program are correlated to the compressibility of the bitstring, where lower scores correlate to higher compressibility.
I am sure that a program could be constructed which would more accurately represent the randomness of a given bitstring. However, I have not yet found a more holistic method. This is something I hope to investigate further.
I have created a much faster C implementation of this program for those who find this useful. It performs exactly the same function but much more quickly, and it is more portable.
the parse interpreted algorithm language
the production of the parse language and its interpreter
20171102
The objective of this project is to create an unornamented algorithm language which has extensive applications in the processing of bitstring inputs. As an important disclaimer, this language is still very much in development, and it is becoming more sophisticated. The language is foreseen to eventually support recursive functions and conditionals, but currently, the language is relatively limited in function.
An algorithm expression will be made which specifies the operations to be evaluated using the bits from specified positions in the bitstring. The interpreter works with the input in segments of the number of characters of the number of variables specified in the expression.
For example, if the bitstring, 00011011, is evaluated with the expression, (0|1)&~(0&1), this will evaluate as follows, in which arrows express levels of evaluation:
(0|1)&~(0&1)->{0,1} (alternatively represented as (a|b)&~(a&b)->{a,b})
->00,01,10,11 each evaluated with the expression
->(0|0)&~(0&0)
->0
->(0|1)&~(0&1)
->1
->(1|0)&~(1&0)
->1
->(1|1)&~(1&1)
->0
This gives the output of 0110.
Expressions comprised of comma-delimited phrases allow for multiple operations to be performed on the same inputs, for example:
0|1,~(0&1)
This expression, when used to evaluate the same bitstring input used in the previous example, will evaluate as follows:
(0|1),~(0&1)->{0,1} (alternatively represented as (a|b),~(a&b)->{a,b})
->00,01,10,11 each evaluated with the expression
->(0|0),~(0&0)
->0,1
->(0|1),~(0&1)
->1,1
->(1|0),~(1&0)
->1,1
->(1|1),~(1&1)
->1,0
This gives the output of 01111110.
If this output were to be evaulated with the expression 0&1, the functional difference between the two preceding expressions, the bitstring would be evaluated as follows:
0&1->{0,1} (alternatively represented as a&b->{a,b})
->01,11,11,10 each evaluated with the expression
->0&1
->0
->1&1
->1
->1&1
->1
->1&0
->0
This gives the output of 0110, similarly to the first expression, because it takes the input in 2-groups and does an and operation on them, which is the functional difference between the previous two expressions.
This algorithm language can be used for many more applications than simply operating with 2-groups from the input bitstrings; operations can be performed using any number of variables less than or equal to the number of bits in the bitstring.
Only the bitring minus the remainder of it and the number of variables given in the expression will be evaluated, since only that part can possibly be evaluated using the given expression. For example, if a bitstring of an odd length is given in conjunction with an expression containing two variables, the remaining bit in the input will be ignored.